Like all objects that do or can move, NASA Sounding Rockets obey Newton's Laws of Motion. The following text provides a very basic summary of the three laws of motion.

Newton's First Law: An object in motion tends to stay in motion and an object at rest tends to stay at rest until acted on by an imbalanced external force.

External Forces - Let's start with the basics. A given object can be acted on by more than one force. An apple hanging on a tree is acted upon by two basic forces: 1) the downward force exerted by the gravity force and, 2) the upward force exerted by the tree limb. The downward gravity force is also know as "weight".

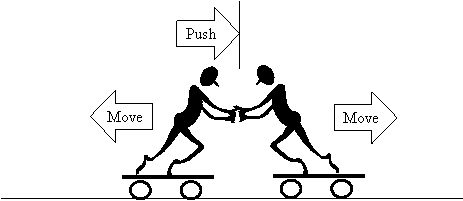
Balanced Forces - Forces can be generated in other ways as well. The two moving men depicted in the figure below are applying two external forces on the box. If both are pushing with the same force, but in opposite directions, the resultant force acting on the box is zero.

From this example, we can see that forces have a magnitude and a direction. Quantities that have both MAGNITUDE and DIRECTION are known as VECTORS. In the case of the two moving men, One can be defined to be pushing in the positive direction while the other is pushing in the negative direction. If both are pushing with a force of 10 Newtons, one is pushing with a -10 Newton force and the other is pushing with a +10 Newton force. Adding these two vector quantities together results in a resultant force of zero.

Mathematically:
Force exerted by the mover on the left = +F
Force exerted by the mover on the right = -F

If we add the two "equal", but "opposite" forces generated by the two movers, the total force is zero.

Total Force = (+F) + (-F) = 0


The end result may be a lot of sweat on the part of both moving men, but the box isn't going to budge! This may become mathematically obvious once we discuss Newton's Second Law of Motion.

Imbalanced Forces - If the mover on the right takes a break, the force becomes unbalanced. Since an external force now exists, the box will begin to move.

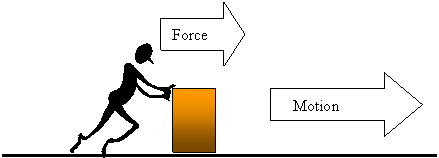
This makes intuitive sense, but Netwon's 2nd Law will show it from a mathematical perspective. Now that we have been reminded of the concept of "external forces" we can now move on to the underlying concept of the First Law - Inertia

Inertia

The First Law is also referred to as the principle of inertia, which is an object's apparent resistance to a change in motion. The word "inertia" is Latin for "laziness" or "idleness". This is a fitting term since the first law relates to and object's "lack of desire" to change its own motion. As stated earlier, objects in motion "want" to stay in motion and objects at rest "want" to stay at rest unless some external force prompts them to change their speed or direction. External forces include friction, gravity or some other pushing or pulling force. These forces can be generated by a baseball bat, rocket motor, pressure imbalance, wind, or a million other things.

Newton's 1st law of motion demonstrates the difference between the Aristotelian worldview and that of Newton. Aristotle assumed that everything had its "natural" position. A rock's natural position is at the center of the Earth, which is why it falls downward when it is dropped. Water's natural position is on the surface of the Earth and that's why it forms pools, puddles and lakes on top of the rock. Air's natural position is above the ground and hence it floats above the surface of the Earth. Newton's 1st law implies that objects have no "natural" position. In the absence of the force of gravity, a rock thrown into the air will move away from the center of the Earth and never fall back. In the absence of the force of gravity, air, rocks and water would float around together and they would have no "natural" position.

The inertia of an object depends on the object's mass. Heavy objects have a high inertia while lighter objects have a low inertia. Since weight is related to the amount of matter contained within an object, more matter equates to more inertia. For example, a mouse consists of a very small amount of matter, and as a result, has a very small inertia. An elephant on the other hand, is composed of a large amount of matter and has a corresponding high inertia. Obviously it is much harder to stop a moving elephant than it is to stop a moving mouse. If you have doubts about this, try stopping a mouse rolling down a hill on a skateboard and then try to stop an elephant on his skateboard. This experiment will make the concept of inertia "painfully" obvious.

Applications

Newton's first law of motion is essentially the basis for all motion. It applies to the trajectory (flight path) of a baseball after it is hit as well as the flight of a rocket.

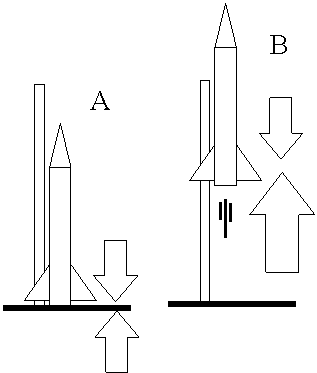
For example, when the rocket is sitting on the launch pad (Figure A), it's weight is exactly opposed by the upward "supporting" force generated by the launch pad. These diametrically opposed forces result in a net external force of zero. Since the rocket is initially at rest and no net external force exists, it will stay at rest. Once the rocket motor is ignited (Figure B), the external force is no longer balanced and the rocket begins to move. In this case, the external thrusting force overcomes the rocket's "desire" to say motionless.

Newton's Second Law: The acceleration produced by a force acting on a body is directly proportional to the magnitude of the force and inversely proportional to the mass of the body.

Most people know this law as "force is equal to the mass times acceleration". As simple as this law sounds, it has some very profound implications. It states that if we know the net external force acting on the body, we can calculate the acceleration of that body.

In its basic form, the equation F=ma probably isn't going to quite register with people. However, if we apply a little algebra, we can transform the equation into a more usable form:

Step 1 - Divide each side by Mass (M)
F / M = (M x a) / M

Step 2 - Cancel the Mass terms on the right hand side
F / M = (M x a) / M

Step 3 - Swap the sides of the equality
a = F / M

This new form of the second law tells us the acceleration of an object is equal to the force acting on the object divided by the object's mass.

Note that this law also deals with "net external forces" and if the net external force is zero, the object will have zero acceleration. This means the object will not speed up or slow down.

Newton's 2nd law is the basis for rocket trajectory simulations. The velocity of the rocket can be obtained by "integrating" the area under the acceleration curve. The acceleration curve (a = F / M) is defined by the weight, thrust, and drag of the rocket at any given time. Integrating the area under the velocity curve yields the distance the rocket has moved. A detailed dissertation of this process will be deferred to a later time.

Applications

The second law can be used to predict how fast a falling ball will be traveling just before it hits the ground and how long it will take to fall. By expanding the "degrees of freedom" of the example and adding appropriate force vectors, we can use Newton's 2nd law to predict the flight path of a rocketship.

Newton's Third Law: For every action there is an equal and opposite reaction.

Most people know Newton's Third Law as the law of "action and reaction". When one object (i.e. a girl) pushes on another object (i.e. a boy), the first object moves in one direction and the second object moves in the opposite direction.

Some scientists do not like this generalized definition of the third law because it tends to focus on the resulting motions rather than the actual forces involved in the phenomena. This general statement also implies that one event (the "action") is more important than, and occurs before, the other (the "reaction"). This may appear to be the case when we consider a child pulling a wagon, but when we consider the case of a thrusting rocket motor, it is not clear if the rocket motor is pushing on the escaping gas or the escaping gas is pushing on the rocket motor. In reality, both actions occur at the same time and it is theoretically impossible to distinguish which object is actually applying the force. As such, it may be better to state the third law in the following manner:

"When one object exerts a force on a second object, the second object exerts an equal and opposite force on the first".

Purists refer to this as the "law of interaction", because the forces involved interact with each of the bodies.

Applications

This law applies to all objects that are undergoing an acceleration. The action of the rocket motor causes the rocket to move in the opposite direction. The child's foot pushing off the ground causes her skateboard to move in the opposite direction.

Newton's second law ties into the third law because we usually equate the action/reaction to the resulting motion that is created as the result of the applied forces. If we know the applied force between the objects and the mass of those objects, we can predict the resulting motion.